５年「速さ」
中学入試にはよく出てくる問題形式です。総じて旅人算などと呼ばれています。
2地点から同時に出発した人同士が出会う状況の問題(出会い算)と、同じ地点から先に出発した人を後から追いかける状況の問題(追いかけ算、追いつき算)などがあります。
中学で学ぶ連立方程式を使えば簡単に求められる答えですが、小学生が解くときは表を書いて変化の様子からきまりを見つけて解きます。
以前の啓林館の教科書では「変わり方を調べて」の単元で扱われていました。
ここでは、啓林館版の問題に似た問題を扱いながら、解き方や教え方を紹介します。
①２つの変化する数や量の変わり方に目をつけ、たし算やひき算の考え方をとらえること
②２つの変化する数や量の変わり方を表や式で表すこと
③表から、変化のきまりをみつけて問題をとくこと
教え方１
変化する様子を表にかいて、変化の変わり方（一定量が増えていくこと）をみつけ、問題の解き方をとらえさせます。
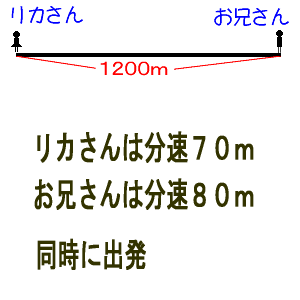
下の問題を例にして、考えさせます
上の問題は出会い算などとも呼ばれています
問題を読ませた後に、問題の場面をとらえさせます↓
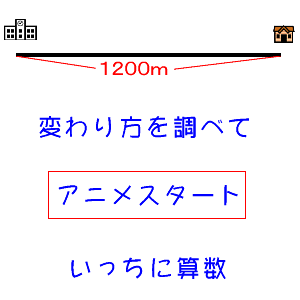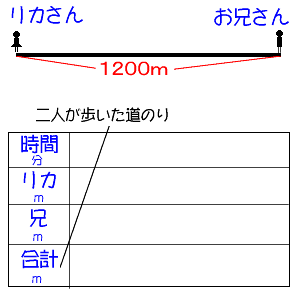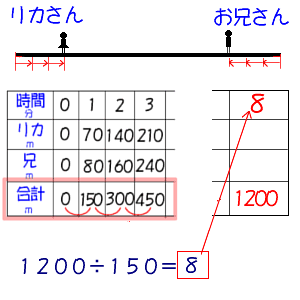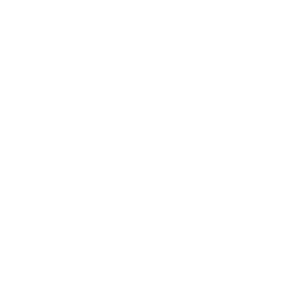
変化の様子を表に整理させます↓
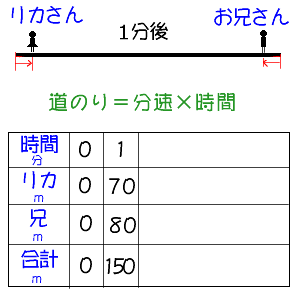
下の表から、１分たつごとに、リカさんとお兄さんの歩いた道のり（距離）の合計は、150ｍずつ増えていることがわかります。
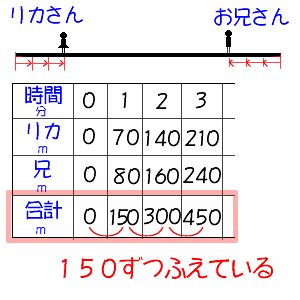
表から、1分間たつと、2人の歩いた道のり（距離）の合計は、150ｍとなる。
学校と家の道のり（距離）は、1200m
なので、式は次のとおりです。
式
70+80=150 1200÷150=8
【答え 8分後に2人は出会う】
たしかめの式
リカさん
７０×８＝５６０ｍ
お兄さん
８０×８＝６４０ｍ
５６０＋６４０＝１２００ｍ
問題に合います
動画で上の問題の解き方を確かめさせます
動画作成協力・・動くイラストフリー素材
教え方２
上の問題の考え方を使って、次の問題を考えさせます。
練習問題
リカさんは家から、お兄さんは図書館から、同じ道を同時に出発しました。家と図書館の間の道のりは2100mあります。
リカさんは分速70m、お兄さんは分速80mで歩きます。
２人は何分後に出会いますか？
式
70+80=150 2人が1分間に歩く道のり
2100÷150=14
【答え １４分後に、２人は出会う】
たしかめの式
リカさん
７０×１４＝９８０
お兄さん
８０×１４＝１１２０
ふたりの合計
９８０＋１１２０＝２１００
問題に合います
次はこちら(追いつき算)をご覧下さい
６年の教え方目次へ
変わり方を調べて(つるかめ算)へ
Copyright 2019 いっちに算数 All Rights Reserved