前のページに戻る
(比とは何か、比の表し方)
比が等しいことの意味と等しい比の性質を教えます。
問題
お母さんと私が酢とサラダ油を混ぜたドレッシングを作りました。作り方は下のようになりました。
二人の作り方のちがいをくらべてみましょう。
お母さんと私が作ったドレッシングの味は同じ味ですか？
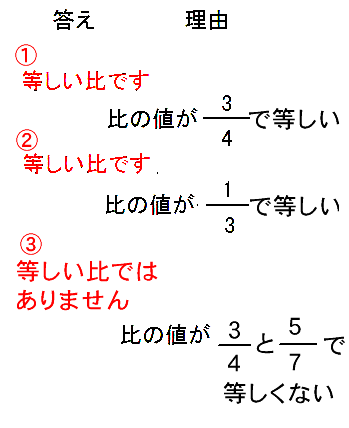
２人の比の値は同じなので、ドレッシングの味は同じになります。
二つの比の値が等しいとき、二つの比は等しいといいます。
二つの比、30：50と60：100が等しいことを
30：50=60：100とかきます
声を出して覚えると
これからの勉強に役立ちますよ
等しい比の間にある関係に気づかせます
等しい比の関係にある秘密①
30：50=60：100の秘密
30：50の両方に2をかけると
60：100になります
等しい比の関係にある秘密②
30：50=60：100の秘密
60：100の両方を2でわると
30：50になります
Ａ：Ｂの両方の数に同じ数をかけたり、両方の数を同じ数でわったりしてできる比は、みんなＡ：Ｂに等しくなります。
声を出して覚えると
これからの勉強に役立ちますよ
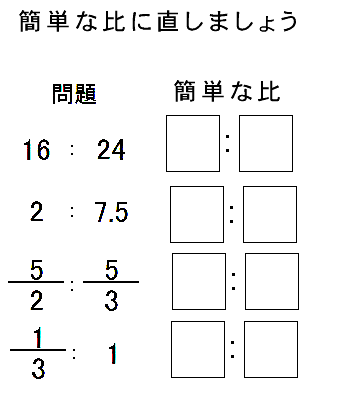
等しい比の秘密を使って、簡単な比にする問題をやってみましょう
問題①
１２：３６を、それと等しい比で、できるだけ小さな整数の比になおしましょう。
１２：３６を両方4で割ると
３：９になりますが、まだ両方３で割れます
すると
１：３になるので
１２：３６＝１：３ です
答え １：３
等しい比で、できるだけ小さな整数の比になおすことを、比を簡単にするといいます
問題②
問題③
下の問題で等しい比はどれですか
また、等しくない比はどれですか
その理由も言いましょう
問題④
問題⑤
比を使って、比べる量と、もとにする量の求め方に気づかせます。問題文が何を聞いているかをしっかりとらえることが大切です。
問題①
ケーキ作りを作りをします。
砂糖と小麦粉の重さの比を2：5にして作ります。小麦粉が200gの時、さとうは何gいりますか。
【線分図を使って求める方法】
線分図を書いて考えることをアドバイスします。考えが浮かばないときは、下の動画を見せて考えさせます。線分図を使う考え方で、問題をといた時は、動画で考え方の確かめをします。
動画作成協力・・動くイラストフリー素材
線分図
小麦粉２００ｇは、２：５の５にあたる量なので、比の１つ分にあたる量は200÷5で、40gということに気づかせます。
さとうは、比の２つ分なので、４０×２で80gとなります。
式 ２００÷５＝４０
４０×２＝８０ 答え 80g
【比の値を使って求める方法】
上にあげた2つの解き方に気づかせ、「答えを出しやすい考え方はどちらかな？」と聞いていくと、比を利用した考え方が、理解できるようになってくると思います。
問題②
はなこさんと妹が2mのリボンを分けます。
はなこさんの分と妹の分の長さの比を3：1にするには、それぞれ、何cmずつに分ければよいでしょう。
【全体をきまった比に分けて考える】
はなこさんの分と全体の長さの比で考えることをアドバイスします。考えが浮かばないときは、下の動画を見せて考えさせます。自分で問題が解けた時は、動画で考え方の確かめをします。
動画作成協力・・動くイラストフリー素材
※ 2mは、200cmです。
妹の分は、全体の200cmから、はなこさんの150cmをひいて、残り50cmとして答えを出すこともできます。
教科書に比の文章問題がありますので、おさらいをしておくと中学の勉強に役立ちます。
最後に
「比」の勉強を家庭で教える時は、文章問題などに最初から取り組むよりも、ドレッシングやめんつゆの配合など、身近な生活場面で、よく使われていることを例に出したほうがわかりやすくなります。
算数ｱﾆﾒは、お子さんが文章題を難しく感じている時に、見せながら説明すると効果的だと思います。
【小学校の先生方への指導補足】
授業づくりや研究授業の参考にしていただければ幸いです。
「比」は「割合」を表す方法の一つですが、百分率での「割合」の表し方と違います。「比」という割合の表し方には、百分率とは違ったよさが、次のようにあります。
【「比」で表すよさ その１】
「比」は、対等に並べられている２つの部分（数量）の割合を表すのに使われます。例をあげると、ある長方形のチョコレートの形を表すのに、「縦は、横の６０％」というより、「縦と横の長さは、３：５」といったほうがわかりやすいという「比」のよさがあります。さらに、縦と横の長さについて、「もとにする量」は、どれかということも考えなくてすみます。
【「比」で表すよさ その２】
これまで同種の量を比べる時は、一方を基準の１としてみて数（整数・小数・分数）で表すことを学んできていますが、「比」は何倍かにすることによって、整数の「比」で表すことができます。また「比」を用いて割合を表すと、基準量を自由に選ぶことができるので、整数だけで関係を表すことができるよさがあると考えます。
【「比」で表すよさ その３】
「比」は、２つの数量の割合を、相互の相対的な大きさに着目して考えていますので、量の大きさそれ自体を切り離して考えることができます。
Copyright 2019 いっちに算数 All Rights Reserved