５年算数
割合の教え方１
子どもの学習支援ｂｙいっちに算数スマホ版

　「割合」は、ある量をもとにして、くらべる量がもとにする量の何倍にあたるかを表した数です。
　この勉強をわかりやすくするためには、「線分図」や「関係図」を使って「割合の３つの用法」をとらえさせたいと思います。

①割合の意味と割合を求める問題の解き方
②割合の考え方で比べる量を求める問題の解き方
③割合の考え方でもとにする量を求める問題の解き方
④百分率%の意味と百分率を使った問題の解き方
⑤帯グラフ・円グラフの読み方と書き方

④百分率・歩合はこちら
⑤帯グラフ円グラフはこちら
教師用ページはこちら

教え方１

　どのクラブに入りたいかという調査の結果から割合の意味を理解させます。

問題
　下の表は、クラブの定員と希望者の人数です。

クラブ名	定員(人)	希望者(人)
スポーツ	１５	３０
オセロ将棋	２０	１０
器楽	１５	２０
まんが	２５	２５

質問
「それぞれのクラブで、希望者は、定員の何倍になっていますか？」
教え方
・希望者は、多くなったり少なくなったりする数ですから「くらべる数」です。
・定員は、いつも同じ数ですから「もとにする数」です。

「くらべる数÷元にする数＝割合(何倍)」です。

スポーツクラブの希望者と定員の関係は、次のようになります。

オセロ・将棋クラブの希望者と定員の関係は、次のようになります。

　ある量をもとにして、くらべる量が、その何倍にあたるかを表した数を、「割合」といいます。

割合は、次の式で求めることができます。

割合＝くらべる量÷もとにする量

　このことから、定員を1とした時、それぞれのクラブの希望者は、次のとおりになります。

クラブ名	希望者÷定員	割合(倍)
スポーツ	30÷15	２
オセロ将棋	10÷20	０．５
器楽	20÷15	１．３３
まんが	25÷25	１

もとにする量・・・定員(変わらない)
くらべる量・・・希望者(変わる)

割合を見れば、どのクラブが希望がとおりやすいかがわかります。
割合(倍率とも言います)が高いスポーツクラブや器楽クラブは希望が通りにくく、オセロ・将棋クラブやまんがクラブは希望者全員が入れることがわかります。

教え方２

　問題文をもとに、全体と部分、部分と部分の割合についてとらえさせます。

問題
たろう君のクラスは、40人ですが、
スポーツクラブに入った人が　30人、
音楽クラブに入った人が　10人です。

問題１
「スポーツクラブに入った人は、クラス全体の何倍ですか？」

教え方
割合の関係にあてはめてみましょう

クラブの人数は、それぞれちがう数ですからくらべる数です。
クラスの合計人数は、変わらない数ですから、もとにする数です。

だから、
「クラブごとの数」÷「クラス合計」が割合になります。

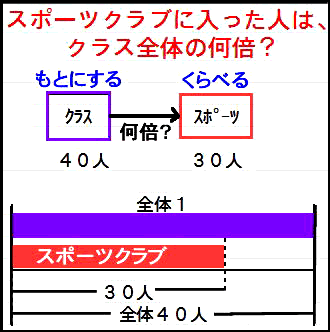
くらべる量はスポーツクラブの30人で
もとにする量はクラス人数の40人です。

式　30÷40＝0.75 　答え　0.75倍
(小数の倍になることもあります)

全体と部分の割合を聞いています

次に部分と部分の割合を聞いている問題です

問題２
「スポーツクラブの人数は、音楽クラブの人数の何倍ですか？」

考え方
スポーツクラブの人数に対して、音楽クラブの人数を聞いています。
割合の関係にあてはめてみましょう

スポーツクラブは、音楽クラブの　何倍ですか　と聞いているので

　スポーツクラブ・・・くらべる数
　音楽クラブ・・・もとになる数
です

求める式は
「スポーツクラブの数」÷「音楽クラブの数」=割合(何倍)となります。

式３０÷１０＝３　　　　答え　３倍

教え方３

　問題文から、もとにする量と割合を使って、くらべる量の求め方を教えます。

問題
　テニスクラブの定員は、15人です。
希望者は、定員の0.8倍です。
希望者は、何人ですか？

教え方
ここでは、元にする数と割合がわかっています。
単純に「○○の２倍は、□□」のように、２倍という数字を使って考えさせると、元の数を割合(２倍)でかけ算すればよいことがわかります。
２倍でも０．８倍でも式は同じということを理解させます。

上の式を変形すると

となります
定員が　もとにする数で
割合が　０．８倍ですから
希望者(くらべる数)は　次の式で求められます。

１５×０．８＝１２　　答え　希望者は１２人