目次
１．単位量あたりの大きさ １＞２
２．速さ １＞２＞３＞４
①単位量あたりの考え方の意味
②広さ（
）や人数、ｶﾞｿﾘﾝ（L）の量や走る道のり（km）などを例に、２つの量の割合で表される量の理解
③単位量あたりの考え方を使ったくらべ方や表し方（人口密度など）
④速さの意味と公式、速さの計算
このページには①と②を掲載しています
③は次のページです
④はこちらのページです
この単元で学習すること
下のペンギンの部屋で、「どの部屋がいちばん混み合っているのかな？２番目はどの部屋かな？」と問いかけます。
| Aの部屋 | Bの部屋 | Cの部屋 |
 |
 |
 |
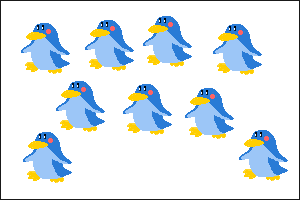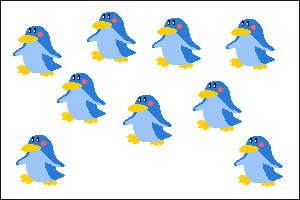| 6で9ひき |
6で8ひき |
5で8ひき |
4年生までは、長さや広さ、かさの大きさを比べる時は、必ず、比べる量の種類は１つでした。
しかし、５年の「単位量あたりの大きさ」の勉強では、上の問題のように、こみぐあいを調べるためには、部屋の広さとペンギンの数という２種類の量を くらべなければなりません。
そこで、量を一つの種類にそろえて比べる勉強をします。
ここが、5年生が理解しにくいところです。そこで、次のように教えていきたいと思います。
１年の「長さくらべ」を思い出させて下さい。
動画作成協力・・動くイラストフリー素材
長さを比べるために端をそろえました。この考えをヒントにします。
なにかを比べる時には「そろえる」ということに気づかせましょう。
下図のペンギンの部屋のこみぐあいの順番を考えることを通して、量を広さや数の単位にそろえて比べる考え方に気づかせます。
問題①
下のペンギンの部屋で、こみあっている順番を考えましょう。
Aの部屋
６で９ひきいます
Bの部屋
６で８ひきいます
Cの部屋
５で８ひきいます
※動画作成・・動くイラストフリー素材
表にすると次のようになります。
| 部屋の面積() |
ペンギンの数(ひき) | |
| Ａ | ６ | ９ |
| Ｂ | ６ | ８ |
| Ｃ | ５ | ８ |
お子さんに予想させ、ＡとＢの部屋のこみぐあいを比較させ、つぎにＢとＣの部屋のこみぐあいを比較させます。
１．ＡとＢの部屋のこみぐあいを比べよう
| Aの部屋 | Bの部屋 |
 |
 |
| ６で９ひき |
６で８ひき |
AとＢの部屋の広さは同じで、ペンギンの数がＡの部屋のほうが多いので、Aの部屋とＢの部屋では、Aの部屋のほうがこんでいるとわかります
２．ＢとCの部屋のこみぐあいを比べよう
| Bの部屋 | Cの部屋 |
| |
 |
| ６で８ひき |
５で８ひき |
ＢとＣの部屋のペンギンの数は同じで、Ｃの部屋のほうが狭いのでＢの部屋とＣの部屋では、Ｃの部屋のほうがこんでいるとわかります。
３．ＡとCの部屋のこみぐあいをくらべよう
| Ａの部屋 | Cの部屋 |
|
|
| ６で９ひき |
５で８ひき |
面積かペンギンの数かどちらかをそろえることができません。
方法１
ペンギンの数１ぴきあたりの面積で比べる
方法２
面積1あたりのペンギンの数で比べる
このことに気づかない時は、教えます。
方法１について
ペンギン１ぴきあたりの面積で比べる
（小数第2位まで求める）
Ａは、6÷9=0.67 1ぴきあたり0.67
Ｂは、6÷8=0.75 1ぴきあたり0.75
Ｃは、5÷8=0.63 1ぴきあたり0.63
答え
１ぴきあたりの面積は、C－A－Bの順でせまいので、こんでいる部屋は、C－A－Bの順です。
いちばん こみあっているCの部屋
つぎに こみあっているＡの部屋
いちばん すいているＢの部屋
方法２について
面積１あたりのペンギンの数で比べる
式 ペンギンの数÷広さ
（小数第2位まで求める）
Ａは、9÷6=1.5 1あたり1.5ひき
Ｂは、8÷6=約1.33 1あたり約1.3ひき
Ｃは、8÷5=1.6 1あたり1.6ひき
答え
１あたりのペンギンの数は、C－A－Bの順で多いので、こんでいる部屋は、C－A－Bの順です。方法１と答えは同じです。
こみぐあいは、「1あたりのペンギンの数」や「１ぴきあたりの面積」のように、２つの量のうち、どちらか一方をそろえると比べることができます。
どちらをそろえても混み具合の順番は同じということに気づかせましょう。
下の表の練習問題を使って、こみぐあいのしらべ方をおさらいします。
問題②
A小学校とB小学校のバレーボール大会に下の表のような参加者がいました。どちらの体育館のほうが混み合っていますか？
一人あたりの面積を比べる方法
A小 450÷45=10 1人あたり10
B小 560÷40=14 1人あたり14
答え
1人あたりの面積は、A小学校の方がせまいので、A小学校のほうがこんでいる。
1あたりの人数を比べる方法
A小 45÷450=0.1 1あたり0.1人
B小 40÷560=0.07 1あたり0.07人
答え
1あたりの人数は、A小学校の方が多いので、A小学校のほうがこんでいます。
※どちらの方法でもA小学校の体育館の方がこんでいるということになります。
続きは、次のページをご覧下さい
単位量あたりの大きさをくらべる問題
速さの教え方はこちらです
Copyright 2019 いっちに算数 All Rights Reserved
