![]()
丂懱愊偺曌嫮偼丄懱愊偺扨埵傗
傪棟夝偝偣傞偲傢偐傝傗偡偔側傝傑偡丅偦偺偨傔偵俀擭乽偐偝乿傗係擭乽捈曽懱偲棫曽懱乿偺曌嫮傪尦偵偟偰峫偊偝偣傞偲棟夝偟傗偡偄偱偟傚偆丅朰傟偰偄傞偍巕偝傫偵偼丄忋偺儕儞僋愭偱偍偝傜偄偝偣傑偟傚偆丅
![]()
嘆懱愊偺堄枴偲扨埵偺巊偄曽
嘇捈曽懱偲棫曽懱偺懱愊偺岞幃偲巊偄曽
嘊梕愊(傛偆偣偒)偺堄枴偲媮傔曽
嘋暋崌恾宍偺懱愊偺媮傔曽
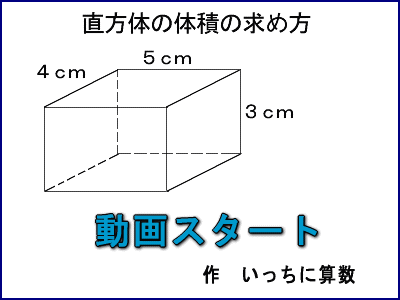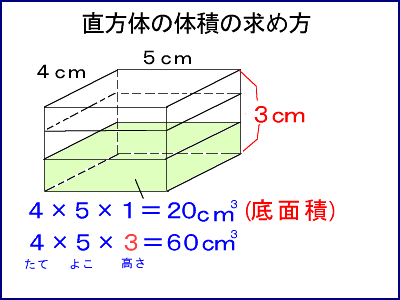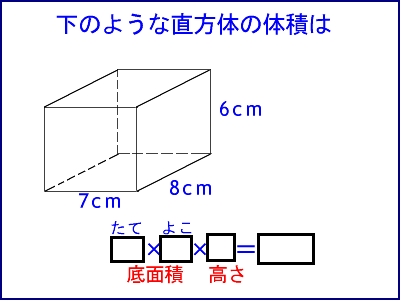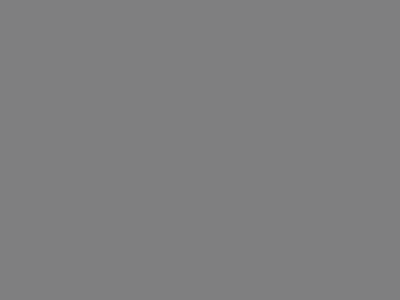
捈曽懱偺偐偝偺戝偒偝偔傜傋傪捠偟偰丄偐偝偺戝偒偝傪侾偺扨埵偱昞偡曽朄傪嫵偊傑偡丅
栤戣丂
壓偺恾偺擇偮偺捈曽懱偺戝偒偝傪偔傜傋傑偟傚偆丅

擇偮偺捈曽懱偼丄幚嵺偵廳偹偁傢偣偰戝偒偝傪偔傜傋傞偙偲偼偱偒側偄偙偲偵婥偯偐偣傑偡丅偱偼丄偳偆傗偭偰偔傜傋偨傜偄偄偺偱偟傚偆丅
![]() 挿偝傗柺愊傗悈偺偐偝傪丂偔傜傋偨偲偒丄偳傫側偙偲傪偟傑偟偨偐丠
挿偝傗柺愊傗悈偺偐偝傪丂偔傜傋偨偲偒丄偳傫側偙偲傪偟傑偟偨偐丠
![]()
擇偮偺捈曽懱偼丄偦傟偧傟侾曈偑侾cm偺棫曽懱偑丄偄偔偮偁傞偐傪挷傋傞偲傛偄偙偲偵婥偯偐偣傑偡丅
壓偺捈曽懱偼丄侾曈偑侾cm偺棫曽懱偑丄侾偩傫偵俉屄偱丄俀偩傫偁傞偺偱丄慡晹偱
侾俇偙偱偡丅
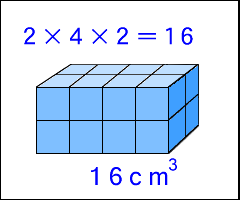
壓偺捈曽懱偼丄侾曈偑侾cm偺棫曽懱偑丄侾偩傫偵俇屄偱丄俁偩傫偁傞偺偱丄慡晹偱
侾俉偙偱偡丅
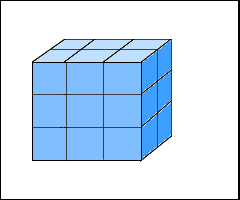
丂丂偙偺偙偲偐傜丄忋偺捈曽懱(崅偝俁cm)偺傎偆偑丄偐偝偑戝偒偄偙偲偑傢偐傝傑偡丅
傑偲傔偺摦夋傪尒傑偟傚偆
摦夋嶌惉嫤椡丒丒摦偔僀儔僗僩僼儕乕慺嵽

嘆傕偺偺偐偝偺偙偲傪懱愊(偨偄偣偒)偲偄偄傑偡丅
嘇懱愊偼丄侾曈偑侾cm偺棫曽懱偑偄偔偮暘偁傞偐偱昞偟傑偡丅
嘊1曈偑1cm偺棫曽懱偺懱愊偼
乽侾乿偲彂偄偰
侾棫曽僙儞僠儊乕僩儖
(傝偭傐偆偣傫偪傔乕偲傞)
偲撉傒傑偡丅
偙偺偙偲偐傜
壓偺捈曽懱偺懱愊偼丄侾俇偲昞偣傑偡丅
壓偺捈曽懱偺懱愊偼丄侾俉偱偡丅
柺愊傗挿偝傗悈偺偐偝偲摨偠傛偆偵丂
傕偺偺懱愊傕丂嫟捠偺扨埵傪巊偭偰昞偡偲丂斾傋傜傟傞偙偲偵婥偯偐偣偰壓偝偄丅
侾丂侾棫曽僙儞僠儊乕僩儖偺撉傒曽傪偟偭偐傝妎偊偝偣傑偟傚偆丅
侾![]() 丂侾暯曽僙儞僠儊乕僩儖偼柺愊偺扨埵偱偡丅傑偪偑偊側偄傛偆偵偟傑偟傚偆丅
丂侾暯曽僙儞僠儊乕僩儖偼柺愊偺扨埵偱偡丅傑偪偑偊側偄傛偆偵偟傑偟傚偆丅

棫曽僙儞僠儊乕僩儖(懱愊偺扨埵) 仩亊仩亊仩 偩偐傜cm偺塃偐偨偵彫偝偔俁傪彂偔丅 暯曽僙儞僠儊乕僩儖(柺愊偺扨埵) 仩亊仩 偩偐傜cm偺塃偐偨偵彫偝偔俀傪彂偔丅 偲妎偊傞偲傑偪偑偊偵偔偄偱偡偹丅 |
捈曽懱傗棫曽懱偺懱愊傪寁嶼偱媮傔傞曽朄偵婥偯偐偣丄懱愊傪媮傔傞岞幃傪嫵偊傑偡丅
栤戣丂
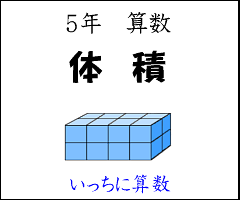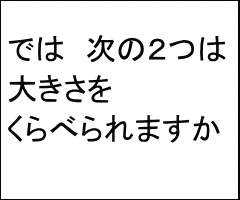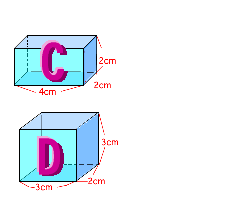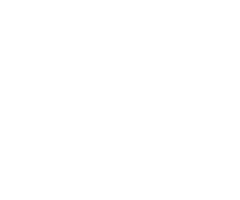
壓偺捈曽懱偺懱愊傪寁嶼偱媮傔傑偟傚偆丅
![]()
忋偺捈曽懱偺懱愊傪寁嶼偱媮傔傞偵偼丄壓偺恾傪尒偰壓偝偄丅
侾偩傫栚偺懱愊傪尒傞偲丄侾曈偑侾們倣偺棫曽懱偑丄偨偰俁屄丄墶俆屄偱俁亊俆偱侾俆屄偁傞偺偱
侾俆偱偡丅
偙傟偑丄忋偵崌傢偣偰係抜偁傞偺偱丄
侾俆亊係亖俇侽丂丂丂丂俇侽偱偡丅

捈曽懱偺懱愊偼
乽偨偰偺挿偝乿亊乽墶偺挿偝乿亊乽崅偝偺挿偝乿偱寁嶼偱偒傑偡丅
乽偨偰丂僇働丂傛偙丂僇働丂偨偐偝乿
偲偍傏偊傞偲丂偍傏偊傗偡偄偱偡偹丅
傑偲傔偺摦夋傪尒傑偟傚偆
栤戣丂
壓偺棫曽懱偺懱愊傪寁嶼偱媮傔傑偟傚偆丅
![]()
忋偺棫曽懱偺懱愊傪寁嶼偱媮傔傞曽朄傪峫偊傑偟傚偆丅
壓偺恾偺傛偆偵丄侾偩傫栚偵丄侾曈偑侾們倣偺棫曽懱偑丄偨偰係屄丄墶係屄偱係亊係偱侾俇偙偁傝傑偡丅侾偩傫栚偺捈曽懱偺懱愊偼侾俇偵側傝傑偡丅
偙傟偑丄係偩傫偁傞偺偱丄
侾俇亊係亖俇係丂俇係偱偡丅
偮傑傝丄棫曽懱偼慡晹偺曈偺挿偝偑摨偠側偺偱丄棫曽懱偺懱愊傪媮傔傞岞幃偼師偺傛偆偵側傝傑偡丅
乽堦曈乿亊乽堦曈乿亊乽堦曈乿亖懱愊
堦偮偺曈偺挿偝傪俁夞偐偗傞偲妎偊傞偲偍傏偊傗偡偄偱偡偹丅

捈曽懱傗棫曽懱偺懱愊傪媮傔傞偵偼丄偨偰丄墶丄崅偝丂傪偼偐偭偰丄偦傟傜偺悢傪偐偗偁傢偣傞偲懱愊傪媮傔傞偙偲偑偱偒傑偡丅

![]()
| 捈曽懱偺懱愊亖偨偰亊墶亊崅偝 棫曽懱偺懱愊亖侾曈亊侾曈亊侾曈 |
岞幃傪巊偭偰師偺懱愊傪媮傔傑偟傚偆丅
嘆丂偨偰6cm墶係cm崅偝俉cm偺捈曽懱
嘇丂堦曈偑俈cm偺棫曽懱
摎偊
嘆丂俇亊係亊俉亖侾俋俀丂摎偊丂侾俋俀
嘇丂俈亊俈亊俈亖俁係俁丂摎偊丂俁係俁
![]()
偙偺懕偒偼丄壓傪僋儕僢僋偟偰壓偝偄
![]() 師偺妛廗偵恑傓
師偺妛廗偵恑傓
![]()
Copyright 2019丂偄偭偪偵嶼悢 All Rights Reserved