５年算数平均わかる教え方１

【はじめに】
　５年生も後半に入りますが、この「平均」から「単位あたりの大きさ」そして、「割合」の勉強になると、急に算数を難しく感じるお子さんがいます。　

「平均」という言葉は、普段の生活で、テストの平均点や平均気温などで使ったりしていますので、子どもにとっては、なじみやすい言葉です。

「平均」の勉強のキーワードは「ならす」
　「平均」は、「いくつかの数やジュースなどの量を合計を変えずにひとつひとつが同じ大きさになるように　ならしたもの」ということをとらえさせれば、「平均」の勉強がわかりやすくなってきます。

①平均の意味
②平均の求め方とその工夫のしかた
③平均を使った長さのおよその求め方
④生活場面で用いる平均のよさ

教え方１

平均の求め方１

　大きさの違う３個のオレンジを絞って、そのオレンジジュースが、１個分では、どのくらいになるかを考えさせ、平均の意味と平均の求め方を気づかせます。

問題１
くまとうさぎとしかがオレンジをしぼったら
ジュースの量が少しずつちがいました。
平均すると何mLですか

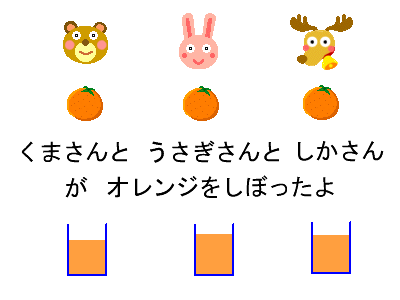
それぞれ、オレンジジュースの量は

170mL 　　240mL　　　190mL
でした。

※mL(ミリリットル)がわからないお子さんには水のかさ(２年)を見せましょう

お子さんに考えたことを言わせて↓の動画を見ましょう。

オレンジジュースを全部合わせると170+240+190=600(合計)
1個分は、600÷3=200
答え　200mL・・・平均

オレンジジュースの全体量は変わらず、一人分の分量が同じになりましたね。これが「量をならす」という考え方、つまり「平均する」ということです。

動画作成協力・・動くイラストフリー素材

グラフの棒の長さを一番長いところから
短いところへ分けることによって
3本の長さを同じにしています。

決まった量の粘土を全部使って、同じ長さの棒を3本作るときも、長い方から切り取ったり、短い方にくっつけたりして同じ長さにすることを体験させるとよくわかります。

　声を出して覚える練習をすると、これからの勉強がわかりやすくなります。

　また、実際に平均を求める場合は、割りきれない数になることが多いので、「4年　がい数」の勉強のおさらいも大切です。
　　　　　　　

教え方２

　「平均の利用」のひとつとして、歩はばを使って、建物の長さのはかる方法を考えさせます。

①太郎君が実際に10歩の距離を5回歩くと、以下のようになりました。

太郎君の10歩分の長さは、6.23mから6.34mと、ばらつきがあります。
これをならすと１０歩分の長さの平均がわかります。
その長さを１０で割れば、太郎君の1歩分の長さ(歩はば)がわかります。

(6.25+6.34+6.23+6.24+6.29)÷5=6.27　　
これは10歩分の長さの平均なので、
１歩分は10で割ると
6.27÷10=0.627 　
0.627mは62.7cmなので
答え　６２．７cm

１ｍ＝100cmを覚えているか確認しましょう。

②太郎君が校舎の長さを歩いてはかったら78歩でした。　
校舎の長さはおよそ何ｍでしょう？
1歩分は６２．７cmなので約６３ｃｍと考えて計算してみましょう。
(平均は、ばらつきのある数の中間の数なのでおよその数で計算していいことを理解させます)

式　
1歩分×歩数＝歩いた距離
６３×７８=４９１４(cm)
４９１４cmは、約４９mと考えられます。

答え　校舎の長さは　約４９m
※もっとわかりやすく約５０ｍと答えてもいいでしょう(現実的です)

このように実際に巻き尺をあててはかれない大きな長さも、歩幅を使ってだいたいの長さがわかると便利だということに気づかせましょう。
　実際に自分の歩幅の平均を求めて、それを使って自宅のまわりの長さを測らせると大変よい勉強になります。
　保護者の方もいっしょにやってみて、正確な設計図との誤差を確かめてみるといいですね。

　平均を求めるとき、割りきれずに小数になることが多いですが、小数点以下や小数第1位以下を四捨五入することも勉強になります。
そういうときに「およその数」「概数」の考え方が実際に役立つことを体験させると算数がおもしろくなります。

1回目	2回目	3回目	4回目	5回目
6.25m	6.34m	6.23m	6.24m	6.29m

５年算数 平均とその求め方 子どもの学習支援 ｂｙ いっちに算数 スマホ版

教え方１

教え方２

５年算数
平均とその求め方
子どもの学習支援ｂｙいっちに算数スマホ版