![]()
嘆丂偁傑傝偺偁傞傢傝嶼偺堄枴
嘇丂偁傑傝偺偁傞傢傝嶼偺寁嶼偺偟偐偨
嘊丂偁傑傝偺偁傞傢傝嶼偺偨偟偐傔偺偟偐偨
嘋丂暥復栤戣偺摎偊偺弌偟曽
偙偺儁乕僕偱偼嘆嘇嘊偵偮偄偰愢柧偟偰偄傑偡丅嘋偼師偺儁乕僕偱偡丅
![]()
嵟弶偵俁擭偺侾妛婜偵曌嫮偟偨乽傢傝嶼乿傪傆傝偐偊傜偣傑偟傚偆丅
仺乽傢傝嶼偺傆傝偐偊傝乿
惗妶応柺偱偺栤戣傪捠偟偰丄偁傑傝偺偁傞傢傝嶼偺堄枴傪嫵偊傑偡丅
栤戣丂
傾僀僗傪侾恖3屄偢偮暘偗傑偡丅
傾僀僗10屄偱偼丄壗恖偵暘偗傜傟傑偡偐丠



摦夋嶌惉嫤椡丂摦偔僀儔僗僩僼儕乕慺嵽
幃丂侾侽亐俁亖俁偁傑傝侾
偙偨偊丂丂丂3恖偵丂偔偽傟偰丄1屄偁傑傞
傾僀僗偑1屄偁傑偭偨偹丂丂
| 戝愗側偙偲 仢俋亐俁亖俁偺傛偆偵偁傑傝偑側偄偲偒偼丄乽傢傝偒傟傞乿偲尵偄傑偡丅 仢侾侽亐俁=俁偁傑傝侾偺傛偆偵丄偁傑傝偑偁傞帪偼丂乽傢傝偒傟側偄乿偲尵偄傑偡丅 |
伀偼丂傢傝偒傟側偄傢傝嶼丂偺椺偱偡丅
係亐俁亖侾偁傑傝侾
侾俈亐俆亖俁偁傑傝俀
(椺丂侾俀亐係偼係偺偩傫偱嬨嬨偺摎偊偑侾俀偵側傞傕偺偼係亊俁偩偐傜丄侾俀亐係亖俁)
椺丂侾俈亐俆傪峫偊傞偲丄俆偺偩傫偺侾俆偑侾俈偵嬤偔偰侾俈傛傝彫偝偄悢偱偡丅
伀俆偺偩傫偺嬨嬨偺昞
偩偐傜丂俆亊俁偺嬨嬨傪巊偭偰
摎偊丂俁丂傪梊憐偟丄
俆亊俁亖侾俆傪丂侾俈偐傜傂偄偰丂
偁傑傝俀丂偲偟傑偡丅
丂丂丂丂丂丂丂丂摎偊丂俁偁傑傝俀

丂嬨嬨偺昞偱偼丄摎偊偺悢帤偲悢帤偺娫偵偁傞悢偼丄傢傝偒傟側偄悢偱偡丅
丂偨偲偊偽伀俁偺偩傫偺侾俇傗侾俈偼丄偦傟傛傝彫偝偔偰嬨嬨偺摎偊偵偁傞悢傪偰偑偐傝偵偟傑偡丅
椺丂17亐俁丂偺峫偊曽
亂侾亃俁偺偩傫偺嬨嬨傪乽俁亊侾偑俁乿偐傜弴偵尵偭偰丄侾俈傛傝彫偝偔偰堦斣嬤偄摎偊傪扵偡丅
丂仺俁亊俆亖侾俆丂偑尒偮偐傞
丂仺俆偑丂摎偊偵側傞
亂俀亃侾俈亅侾俆傪峫偊傞
丂仺侾俈亅侾俆亖俀
丂仺俀偑偁傑傝偵側傞
亂俁亃摎偊傪彂偔
丂仺17亐俁亖俆偁傑傝俀
傑偲傔傞偲
亂侾亃傢傞悢偺嬨嬨傪侾偐傜弴偵尵偆
亂俀亃傢傜傟傞悢傛傝彫偝偔偰嬤偄悢傪尒偮偗傞丂(傢傞悢亊仩偺仩傪尒偮偗傞)
亂俁亃傢傜傟傞悢偐傜偦偺悢傪堷偔(仮)
亂係亃仩偑摎偊偱仮偑偁傑傝
偁傑傝偺偁傞妱傝嶼偼偡傋偰仾偺弴彉偱峫偊傑偡丅姷傟偰偒偨傜丄嬨嬨傪乽亊侾乿偐傜尵傢側偔偰傕嬤偄悢偺嬨嬨傪尵偭偰傒偮偗傜傟傞傛偆偵側傝傑偡丅
偱偡偑丄嬨嬨偺埫婰偵晄埨偑偁傞偍巕偝傫偼丄亊侾偐傜弴偵尵傢偣偨曽偑傑偪偑偊傑偣傫丅
偁傑傝偺偁傞傢傝嶼偼庤弴偑懡偄偺偱丄側傟傞傑偱傑偪偑偊傗偡偔側傝傑偡丅偦偙偱伀偺摦夋偺傛偆偵巚峫偺搑拞宱夁傪墧昅偱栤戣偺壓偵彫偝偔彂偒崬傓偲栚偱尒偰巚峫偑妋偐傔傜傟傞偺偱娫堘偄偑尭傝傑偡丅
侾俈亐俁傪椺偵傗傝偐偨傪愢柧偡傞摦夋伀


偙偆偟偰搑拞偺峫偊曽傪巆偟偰偍偔偲丄摎偊偑娫堘偭偨偲偒丄恊偑偳偺庤弴偱傑偪偑偊偰偄傞偺偐偑傢偐傝丄嫵偊傗偡偄偱偡丅

偨偲偊偽伀偺椺偱偼丄偐偗嶼偺嬨嬨偺慖傃曽偑傑偪偑偭偰偄傑偡丅
伀偺椺偱偼俁偺偩傫偱傕侾俈傛傝彫偝偡偓傞嬨嬨傪慖傫偱偟傑偭偰偄傑偡丅
伀偺椺偱偼丄嬨嬨偼惓偟偄偗傟偳摎偊偑偪偑偆偺偱偁傑傝偑偪偑偆摎偊偵側偭偰偟傑偭偰偄傑偡丅
懠偵傕嵟屻偺傂偒嶼偱傑偪偑偊偨傝偡傞偙偲傕偁傝傑偡丅
惓偟偄傗傝偐偨伀
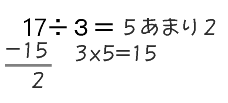
埲忋偺傛偆偵巚峫偺宱夁傪栤戣偵彂偒崬傑偣傞偲娫堘偄傪尭傜偟偨傝丄恊偑偙偳傕偺偮傑偯偒偵婥偯偒側傝傗偡偔側傞偺偱曋棙偱偡丅
傑偨丄偁傑傝偺偁傞傢傝嶼偱偼丄壓偺傛偆偵乽偨偟偐傔嶼乿傪偡傞廗姷傪偮偗偝偣偰偍偔偲帺暘偱娫堘偄偵婥偯偗傞傛偆偵側傝傑偡丅
亂偁傑傝偺偁傞傢傝嶼偲偨偟偐傔偺幃亃
壓偺傛偆側娭學偑偁傝傑偡
偨偲偊偽丂17亐俁亖俆偁傑傝俀偺応崌偼
俁亊俆亄俀亖侾俈偲側傝傑偡丅
伀偺傛偆側娭學偱偡丅
![]()
丂偁傑傝偺偁傞妱傝嶼偺寁嶼偼丄偐側傜偢偨偟偐傔偺寁嶼傪偡傞傛偆偵廗姷偯偗傞偲丂娫堘偄偵帺暘偱婥偯偗傞傛偆偵側傝傑偡丅傑偨丄妱傝嶼偲偐偗嶼偺娭學傕傢偐偭偰偒傑偡丅

偍巕偝傫偵妋偐傔傑偟傚偆丅
仸丂傢傝嶼偺摎偊傪弌偡帪偼丄嬨嬨傪巊偭偰峫偊傞偲摎偊偑弌偟傗偡偄偙偲偑棟夝偱偒傑偟偨偐丅
仸丂偁傑傝偺偁傞妱傝嶼偺庤弴偵姷傟傑偟偨偐丅
仸丂傢傝嶼偺偁傑傝偼丄偄偮傕傢傞悢傛傝彫偝偄偙偲偵婥偯偒傑偟偨偐丅
偦偺偨傔偵偼丄偍偐偟傗偍嬥側偳幚暔傪巊偭偰偁傑傝偺偁傞傢傝嶼傪嫵偊傞偲傢偐傝傗偡偔側傝傑偡丅
Copyright 2019丂偄偭偪偵嶼悢 All Rights Reserved